This post is adapted from a post I made on Threads in June 2024.
Western music notation presents a clean system: twelve equally-spaced semitones, octaves that double in frequency, and familiar scales built from those building blocks. But when instruments actually vibrate, the math gets messy. The harmonic series—pure physics—doesn't quite align with our equal-temperament tuning grid, and that mismatch forces every performer to make tiny, constant compromises.
The Musical Grid
Music notation organizes sound into discrete steps. We start with the familiar major scale: do-re-mi-fa-so-la-ti-do, or C-D-E-F-G-A-B-C. From the first C to the second C is an octave, and we number them to keep ranges straight—C1 in the bass clef is nowhere near C5 up top.
The spacing between these notes isn't uniform. In the major scale, most steps are "whole steps," but E to F and B to C are "half steps" (semitones). We can fill in the gaps with sharps and flats to get a chromatic scale: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C. That's twelve equally-spaced semitones spanning one octave.
You can hear the difference between the major scale and the chromatic scale—the chromatic version moves in smaller, evenly-spaced steps.
Equal Temperament
Sound is vibration, and we measure it in frequency. An octave means doubling the frequency: if C1 vibrates at 1 Hz (a hypothetical example—real concert pitch sets A4 at 440 Hz), then C2 is 2 Hz, C3 is 4 Hz, C4 is 8 Hz. The mathematical relationship is $f_{\text{octave}} = 2^n f_{\text{base}}$.
But what about the notes in between? Equal temperament solves this by spacing the twelve semitones logarithmically. Each semitone multiplies the previous frequency by $2^{1/12} \approx 1.0595$. Climb twelve semitones and you've multiplied by $(2^{1/12})^{12} = 2$—exactly one octave.
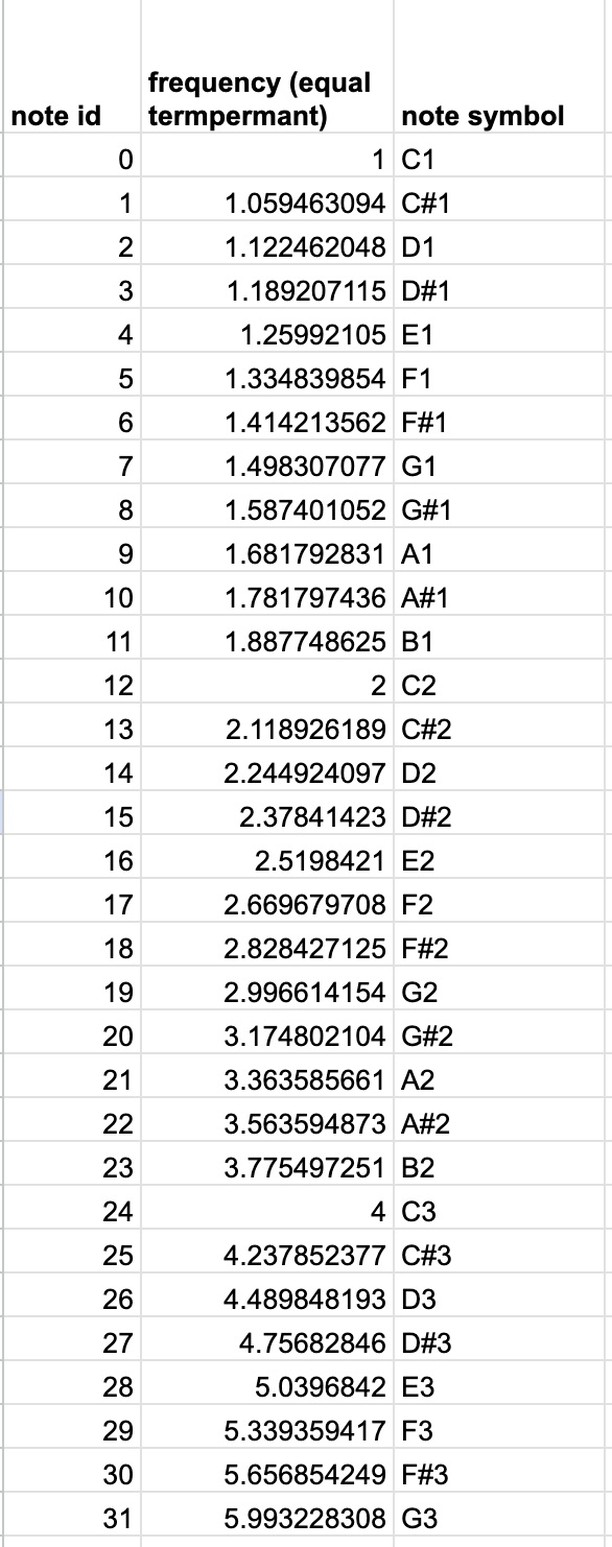
This system is elegant and practical: it works equally well in every key, which is why pianos can modulate freely and orchestras can tune to a single reference pitch.
How Instruments Actually Work
When you pluck a guitar string, it vibrates at a resonance frequency determined by its length, tension, and mass. Halve the vibrating length—say, by fretting at the 12th fret—and you double the frequency, producing a note one octave higher. All those fret markers and harmonic touch points come from this geometry.

But a vibrating string doesn't just produce one frequency. It simultaneously generates integer multiples: 2×, 3×, 4×, 5×, 6×, and so on, each quieter than the last. These are called harmonics or overtones, and they're governed by wave physics—any vibrating object does this. The mix of harmonics gives each instrument its unique timbre, which is why a clarinet and a flute sound different even when playing the same written note.
The Mismatch
Here's the problem: those natural harmonics don't line up with our equal-temperament grid.
When you play a C, the harmonics include frequencies close to E, G, and A#—but they're off by varying amounts. The fifth harmonic leans toward E but sits 14 cents flat. The seventh harmonic falls somewhere between A and B♭, missing both by about 30 cents. Equal temperament pretends these notes sit exactly on the grid, but physics disagrees.
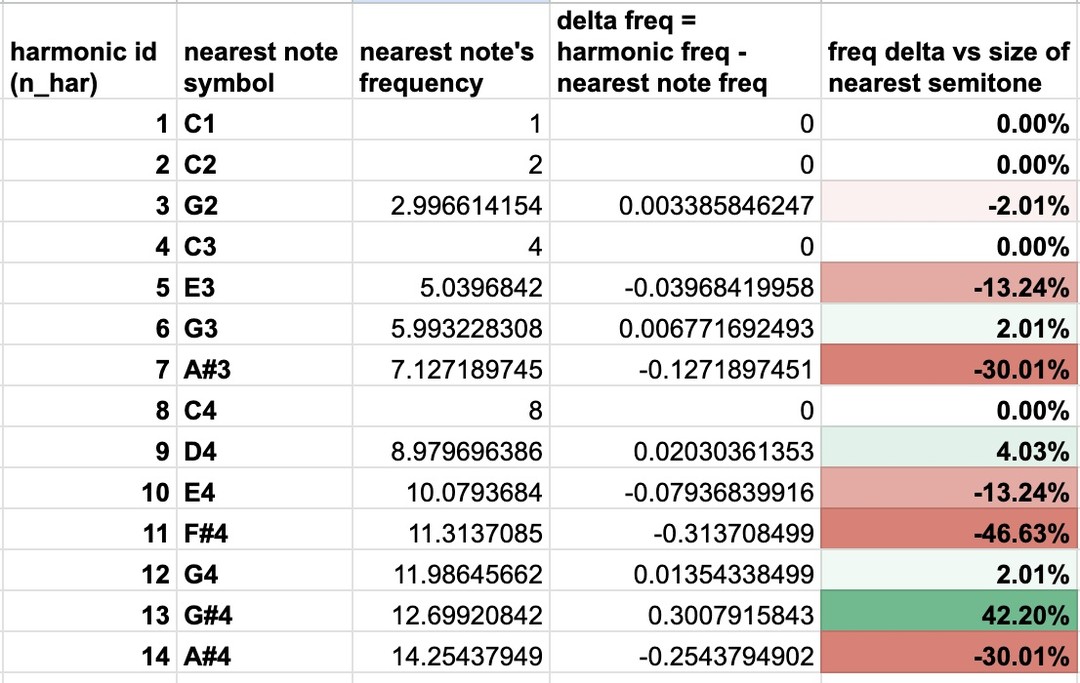
This mismatch explains some musical mysteries. Triads like C-E-G sound harmonious partly because those notes appear in each other's harmonic series, even if not perfectly. But it also means equal temperament is a compromise—a system that works "well enough" everywhere rather than perfectly anywhere.
Living with the Compromise
String players, vocalists, and brass ensembles have the freedom to shade pitches, and many do exactly that. In a cappella singing or a string quartet, performers can lean toward just intonation—tuning intervals to match the pure ratios of the harmonic series—for sweeter chords. But push too far and the tonal center drifts, especially in longer pieces with modulations. It's a constant balancing act.
Keyboard instruments don't have that flexibility. Pianos are stuck with their tuning, though technicians can prep instruments in alternate temperaments when a specific repertoire calls for it. Modern digital keyboards make this easier—some can switch between equal, Pythagorean, mean-tone, and other historical temperaments with a button press.

Equal temperament won out because it's versatile. Baroque composers like Bach wrote collections (the Well-Tempered Clavier, for instance) explicitly to demonstrate that equal temperament made all keys usable. But the physics-music dilemma remains: our notation system will always be an approximation of the messy, beautiful reality of vibrating objects.
